Calculating the Composite Scores (Technical)

This post covers the technical aspect of calculating the SEA composite score. This post is specifically about the calculations, since the math might not be for everyone.

TL:DR:

Actual formula:

Composite = 200 + ( 15*Zm + 9*Zl + 6*Zcw )

Where Zm, Zl and Zcw are the Z-scores for Mathematics, Language Arts and Creative Writing respectively.

Workable-estimate formula:

Composite = 200 + (30 * [Student weighted % - Year's mean %] / Year's Standard deviation)

2025 formula:

2025 Composite Score = 200 + (30 * [Student weighted % - 57.32%] / 23.82%)

I have another post about interpreting the SEA composite scores.

------------------------------------------------

Long explanation:

What is the "composite score" for SEA:

The composite score is the sum of the weighted standard scores.

Wait, what? What are "weighted standard scores".

The weighted standard scores are the standard scores weighted as follows: 100% Mathematics, 60% Language Arts, 40% Creative Writing.

AGAIN, wait! what are the "standard scores" !!

The standard scores are the raw marks contextualised to the number of standard deviations away from the mean, and then averaged to 100. The formula is below:

Standard score: 100 + 15 * Z

Where Z is the Z-score for the subject.

Where did you get this information from? WHAT IS YOUR SOURCE

Source is the MoE: Here is a video where it was spelled out during this year's pre-SEA Q&A session by the MoE:

https://youtu.be/bM9_nuGPoDo?t=3106

(Youtube: "Preparing for Secondary Entrance Assessment" - Ministry of Education - TT - March 17, 2025, relevant part @ 52-minute mark.)

Okay, okay, I believe you, so tell me the formula for the Composite score !!

Composite = 100% Math Standard Score + 60% ELA standard score + 40% CW Standard score

Composite = 100%* (100 + 15*Zm) + [ 60% * (100 + 15*Zl) ] + [ 40% * (100 + 15*Zcw) ]

Where Zm, Zl and Zcw are the Z-scores for Mathematics, Language Arts and Creative Writing respectively.

Okay, but this isn't very usable for me. How Can I calculate a composite from a raw % (or vice versa)?

The formula can be expanded and then simplified to:

Composite = 200 + ( 15*Zm + 9*Zl + 6*Zcw )

Where Zm, Zl and Zcw are the Z-scores for Mathematics, Language Arts and Creative Writing respectively.

Examining that formula will tell you that a composite score for a student completely average in all subjects will be exactly 200, since Z-scores are 0 at the mean value.

A More practical formula still:

Since we normally don't have the standard deviations for each subject, we can't calculate the Z-scores for each subject.

But !! we can try another approach to solve using only the values printed on the SEA slip.

Okay, let's the take above formula and attempt to get it down to just one unknown variable:

Composite = 200 + ( 15*Zm + 9*Zl + 6*Zcw )

Composite = 200 + 30 * [ 50%*Zm + 30%*Zl + 20%*Zcw ]

Now, what I'm going to do here is to combine the [50% Math Zscore, 30% ELA Zscore and 20% CW Zscore] into a single "weighted" Z-score across all subjects. This will simplify the formula to 1 unknown variable allowing us to work with it, at the cost of some precision in the estimate.

Composite = 200 + 30 * (Weighted Z-score)

The insight you can gleam here is that a score of 200 is exactly at the average raw marks, a score of 230 is exactly 1 standard deviation above the average raw marks. A score of 260 is two standard deviations above the average raw marks.

Next, let's expand that weighted Z-score to its functional parts.

Composite = 200 + (30 * [Student weighted % - Year's mean %] / Year's Standard deviation)

The year's mean marks are printed on the SEA slip. The standard deviation is not printed, but since it is the only unknown, we can rearrange and solve for it.

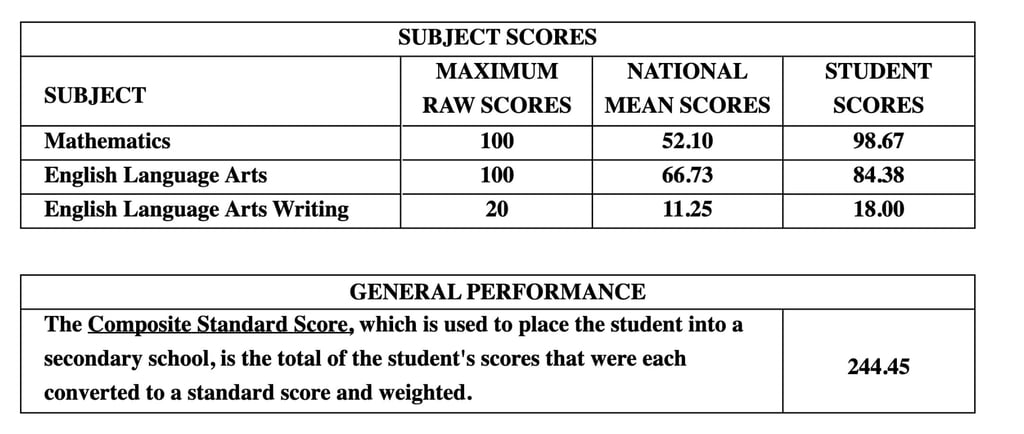
Here is the results on a real, verified SEA slip from SEA 2025, for example.

Math: 98.67%, ELA: 84.38%, CW: 90%; Composite score 244.5

Student's Weighted % = 50%*98.67 + 30%*84.38 + 20%*90 = 92.65%

Year's weighted mean % = 50%*52.1 + 30%*66.73 + 20%*(11.25/20) = 57.32%

Solving to find standard deviation for 2025:

244.5 = 200 + (30 [92.65 % - 57.32 %] / Year's Standard deviation)

Year's (2025's) standard deviation = 23.82.

Re-writing that with all values now known,

2025 Composite Score = 200 + (30 * [Student weighted % - 57.32%] / 23.82%)

You can go ahead and use that to get really close approximate to 2025's results. I've tested it out looking at a few dozen 2025 results and it holds up really well. Here are some results here: https://www.facebook.com/groups/seaparentsupport/posts/4146229322281224/ (private group)

Here is what it looked like for different %'s on the 2025 exam

raw% 2025 Composite score

100% 254

95% 247

90% 241

85% 235

80% 229

75% 222

70% 216

65% 210

60% 203

55% 197

50% 191

45% 184

40% 178

35% 172

.